感知机

一个感知机相当于数字电路里面的一个门电路，多层感知机实现完整电路，以下是与门、与非门和或门的基础实现代码以及原理。如果使用横坐标为$x_1$，纵坐标为$x_2$的数轴来表示，你会发现实际上是$w_1x_1+w_2x_2+b=0$这条直线直线将两块区域划分开来，一部分为0，另一部分为1。
$$
y=\begin{cases}
0, &(b+w_1x_1+w_2x_2 \leq 0)\\
1, &(b+w_1x_1+w_2x_2 > 0)
\end{cases}
$$
其中$b$称为偏置,$w_1$和$w2$称为权重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
def AND(x1,x2):             #与门的实现
    x=np.array([x1,x2])     #输入
    w=np.array([0.5,0.5])   #权重
    b=-0.7                  #偏置
    tmp=np.sum(w*x)+b       #判断
    if tmp <= 0:
        return 0
    else:
        return 1
    
def NAND(x1,x2):            #与非门的实现
    x=np.array([x1,x2])     #输入
    w=np.array([0.5,0.5])   #权重
    b=0.7                   #仅偏置与and不同
    tmp=np.sum(w*x)+b       #判断
    if tmp <= 0:
        return 0
    else:
        return 1
    
def OR(x1,x2):              #或门的实现
    x=np.array([x1,x2])     #输入
    w=np.array([0.5,0.5])   #权重
    b=-0.2                  #仅偏置与and不同
    tmp=np.sum(w*x)+b       #判断
    if tmp <= 0:
        return 0
    else:
        return 1

def XOR(x1,x2):
    s1=NAND(x1,x2)            #通过与非门、或门、与门实现异或
    s2=OR(X1,x2)
    y=AND(s1,s2)
    return y

for x in range(0,2):
    for y in range(0,2):
        print(XOR(x,y))

神经网络

基本概念

神经网络构成：最左边输入层，中间所有部分统称为中间层（也称为隐藏层），右侧为输出层。e.g.上面提到的$x_1$和$x_2$为两个输入神经元（第0层），连接着中间的两个NAND和OR神经元（第1层），再连第二个中间层AND神经元（第2层），最后输出（第3层）。

激活函数将输入信号的总和转换为输出信号，类似中间层的处理函数，下面介绍几种常见的激活函数。

激活函数

  • 阶跃函数
    $$
    y=\begin{cases}
    0, &(x \leq 0)\\
    1, &(x > 0)
    \end{cases}
    $$
    Figure_1

    代码实现：

    1
    2
    3
    def stepfunction(x):
        y=x>0
        return y.astype(np.int64)

  • Sigmoid函数

$$
h(x)=\frac{1}{1+e^{-x}}
$$

Figure_1

代码实现：

1
2
def sigmoid(x):
    return 1/(1+np.exp(-x))

观察函数图像可以发现，阶跃函数和sigmoid函数分别是曲线与折线，都属于非线性函数，而形如$y=ax$的线性函数，在嵌套当中无法发挥更好的作用（$y=h(h(h(x))$可以写成$y=a^3*x^3$),激活函数都是非线性函数。

  • ReLU函数

$$
h(x)=\begin{cases}
0, &(x \leq 0)\\
x, &(x > 0)
\end{cases}
$$

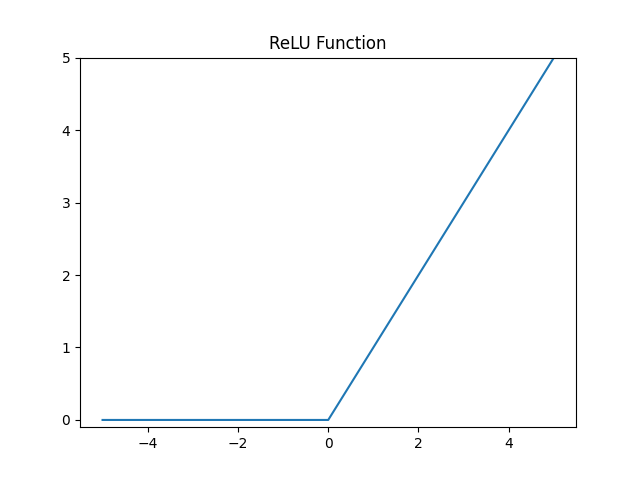
Figure_1

代码实现：

1
2
def relu(x):
    return np.maximum(x,0)

在处理分类问题和回归问题时，可以调整激活函数：回归问题用恒等函数，分类问题用$softmax$函数

  • Softmax函数

$$
y_k=\frac{e^{a_k-C}}{\sum_{i=1}^n{e^{a_i-C}}}
$$

这个式子表示假设输出层有有$n$个神经元，求第$k$个神经元的输出。为了防止溢出所以通常在指数位减去一个较大的数C来平衡，一般会使用输入信号中的最大值。由于输出在0到1之间，所以一般该函数都用于表示概率，即分类为某个物体的概率。

代码实现：

1
2
3
4
5
6
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y= exp_a/sum_exp_a
return y

神经网络的实现

通过矩阵点乘的方式能够将输入根据权重计算到下一层，实现神经网络的向前推进

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np
def init_network():
    network={}  #字典变量
    network['W1']=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])   #第零层有两个输入，三个输出
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])  #第一层三个输入，两个输出
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])  #第二层两个输入，两个输出
    network['b3'] = np.array([0.1, 0.2])
    return network
def forward(network, x):
    w1, w2, w3=network['W1'],network['W2'],network['W3']
    b1, b2, b3=network['b1'],network['b2'],network['b3']
    a1=np.dot(x,w1) + b1
    z1=sigmoid(a1)  #激发函数处理
    a2=np.dot(z1,w2) + b2
    z2=sigmoid(a2)
    a3=np.dot(z2,w3) + b3
    y = a3
    return y
network=init_network()
x=np.array([1.0,0.5])
y=forward(network,x)
print(y)    #[0.31682708 0.69627909]

总结

前面都是一些比较通俗易懂的内容，可以过的比较快，重点还是要掌握如何使用python语言去处理数据，对于模型原理更偏向于数学方面，需要有良好的线性代数以及相关的数理统计知识。